In my last post, I detailed most of the Graphics class settings/values and some tips for getting the best balance of performance and quality. In this post I’ll be examining the InterpolationMode values in detail. The short version of this post is that if you want to get the best quality from System.Drawing/GDI+, use InterpolationMode.HighQualityBicubic. But if you’re curious as to what that means or what the other values mean, read on.

I won’t be doing sample comparisons of the various interpolators’ output because that’s already been done, and I don’t have much to add to that. This is more of a technical analysis of the exact implementations and parameters used and how they compare with the standard definitions of those algorithms.

This post assumes you have a basic understanding of image resampling algorithms and want to see what the GDI+ implementation actually does compared to other software. If you’re not familiar with image resampling terminology or methods, I’d suggest starting with Jason Summers’ excellent article “Basics of Image Resampling”. Once you’ve read that, you may also find his “What is Bicubic Resampling?” enlightening. And if you want to completely geek out on the various standard interpolation algorithms, you can’t go wrong with ImageMagick’s Resampling Filters page. I’ll be linking to that one a lot as I go through the individual interpolators. They have detailed explanations and sample images to go with most.

For my analysis of the GDI+ implementation, I’ll be using the ResampleScope utility, also by Jason Summers. It’s a great piece of software. If he had a donate button on his site, I’d totally click it.

InterpolationMode.NearestNeighbor

There’s not much to say about this one nor I can I show a graph of it like I will with the rest. It’s the fastest and lowest quality interpolator available. Also sometimes referred to as a Point Filter, it simply maps each pixel in the destination image to the nearest corresponding pixel in the source image. The results will be blocky, but when dealing with enlargements of a blocky source, that may actually be desirable. It shouldn’t be used for downscaling. The GDI+ implementation is completely standard and its output matches my implementation in MagicScaler pixel-for-pixel.

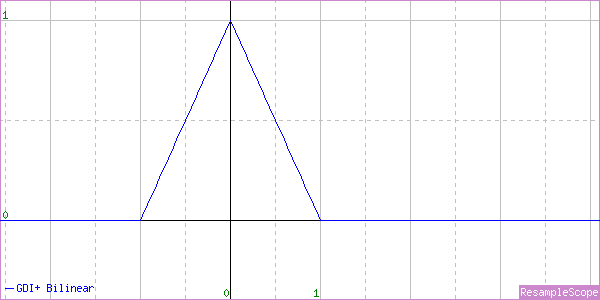
InterpolationMode.Bilinear

The Bilinear (also commonly known as Linear, Tent, or Triangle) interpolator is another completely standard implementation. As long as you’re enlarging, that is…

Yep, that’s a perfectly normal Triangle Filter, all right.

These graphs are fairly large, so I’m showing them at half size.  You can click the images to embiggen them if you like.

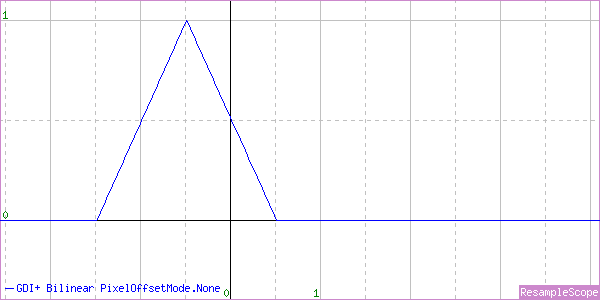
One of the neat things about ResampleScope is that it will also show you when the sample points are calculated incorrectly. For example, if I set the GDI+ PixelOffsetMode to None, here’s what the graph looks like:

The shape is right, but it’s not centered at 0, so it will shift the image up and left. We saw that in the previous post. I’ll be using the correct PixelOffsetMode.Half from now on. I just wanted to show that once. An eerily similar graph will appear in my upcoming breakdown of the WIC interpolators as well.

The documentation for InterpolationMode has an interesting note for the Bilinear value.

“This mode is not suitable for shrinking an image below 50 percent of its original size”.

Let’s see why that is, shall we?

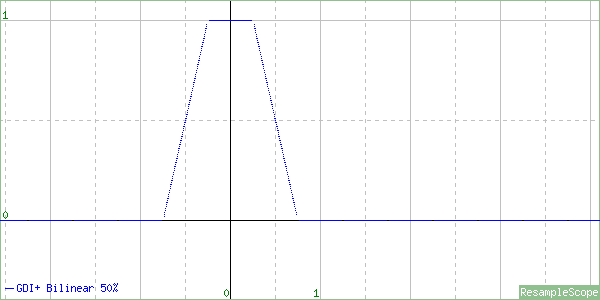
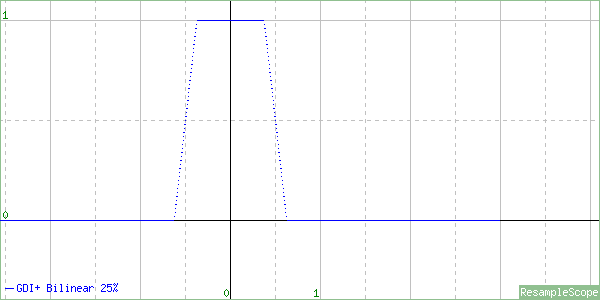
This graph is from a resize to 50% of the original size. Notice that we no longer have a triangle. The top is cut off, plus it’s squished in at the bottom. In a properly implemented scaler, we would expect that the shape of the graph would be the same regardless of the resize direction or ratio. Here’s the graph for a resize to 25%

Essentially, this interpolator is devolving toward a Box Filter the more we shrink the image. This interpolator will produce aliased output. That’s what happens when the edges of the sample range (also known as the filter support) don’t extend to at least ~.75px in each direction, which is about where it was on the 50% shrink. This interpolator is fine for enlarging, but you probably don’t want to use it for shrinking unless speed is more important to you than quality.

InterpolationMode.Bicubic

Having gotten a taste of the Bilinear interpolator, I think I can guess what we’re going to see with Bicubic. We’ll jump straight into the graphs.

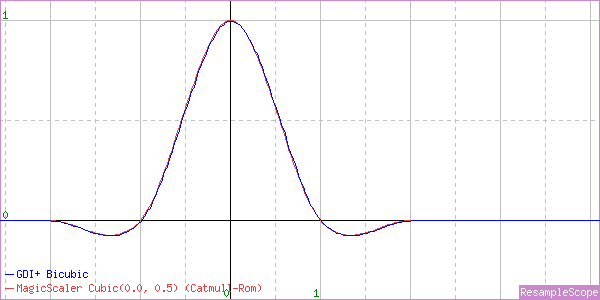
For enlarging, we have a perfectly normal Cubic Filter. I can compare the shape of the curve to that of a known configuration from MagicScaler to get a more precise definition. ResampleScope lets me overlay those together to compare them easily. This one is a near-perfect match for the MagicScaler implementation of the Catmull-Rom (B=0, C=0.5) Cubic – a nice choice.

Let’s see what happens when we shrink to 50%.

Gross. That’s no good for nobody. And 25%?

Also gross. In the docs for this one, there’s a note saying it’s unsuitable for shrinking below 25%, but I’ll just go ahead and say this one’s really unsuitable for shrinking at all. In fact, this one is worse than Bilinear for shrinking. It will, however, give nicer, sharper results for enlargements.

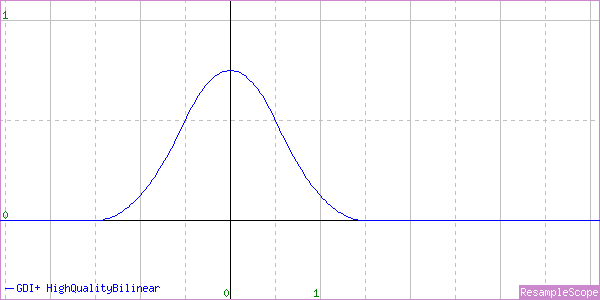
InterpolationMode.HighQualityBilinear

What we’ve seen so far are quite standard implementations of well-known resampling algorithms that simply aren’t scaled fully for shrinking images. That makes them faster, but they sacrifice quality. We can probably assume that the HighQuality variants are correctly scaled, though. The documentation has the following note on both of the HighQuality options:

“Prefiltering is performed to ensure high-quality shrinking”.

That’s vague and mysterious, but let’s see what the graphs say, starting with an enlargement.

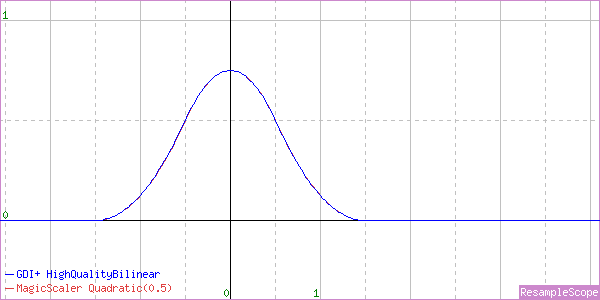
Well, that’s interesting… It’s not even close to linear. It looks more like a Quadratic Filter, and sure enough it’s a dead ringer for MagicScaler’s Quadratic implementation with its blurriest setting.

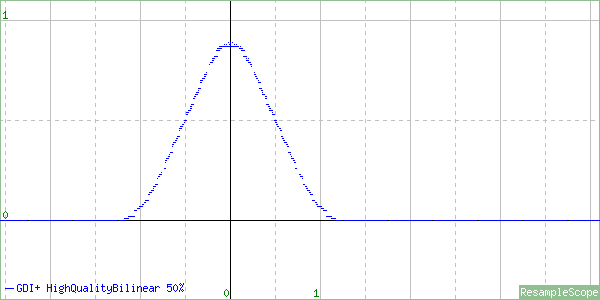
But the real test is the downscaling, so let’s see what happens there.

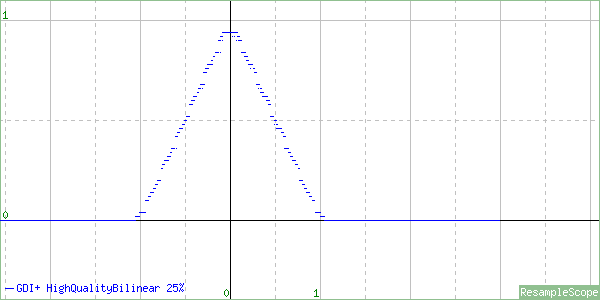
Much like the low quality modes, at 50% it appears to be just squeezing the filter in, although it still has a large enough support range to give good quality at this size. Let’s see 25%.

What do you know… it appears to be converging on an actual Linear filter.

So it turns out the HighQualityBilinear filter is actually a blurry Quadratic for enlarging and minor shrinking but becomes a Linear for higher-ratio shrinking. This is a perfectly cromulent interpolator. It’s suitable for all uses as long as you don’t mind the blurring.

As for the prefiltering they mentioned, the discontinuities in the graph may be a reflection of that. ResampleScope will sometimes show gaps in the graph for higher-ratio shrinking, but the gaps in these graphs are abnormally large. My guess is they’re doing a blur before resizing. You can approximate a correctly scaled resampling filter by blurring the source image first and sampling a smaller range. They may be doing that instead of scaling the filter up all the way. The results end up similar, so I’ll take their word for it. That may also be a clue to the poor relative performance of this interpolation mode. In my testing, it has often been slower than HighQualityBicubic despite the fact that it has a smaller sample range.

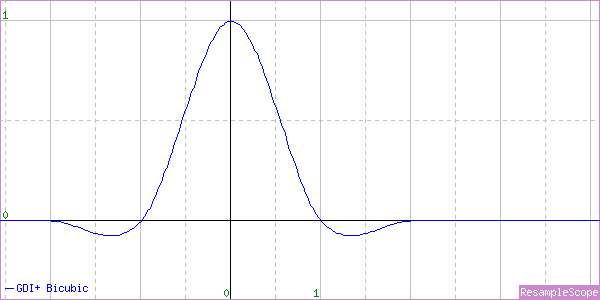
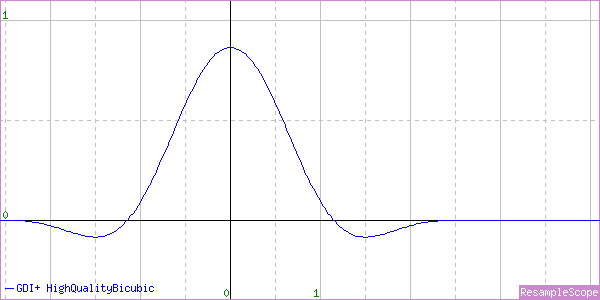
InterpolationMode.HighQualityBicubic

We already know this is the best one, but let’s see what it actually does. As before, we’ll enlarge first.

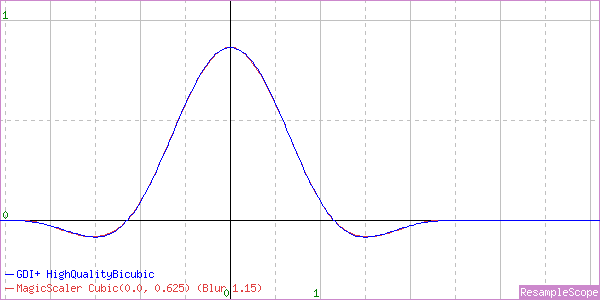
We would normally expect a Cubic to have a support of 2px, and this one reaches just beyond that. The closest match I could find with MagicScaler was a nonstandard Cubic (B=0, C=0.625) with a blur factor of 1.15, which means the normal sample range is simply stretched by 15%, giving a smoothing effect.

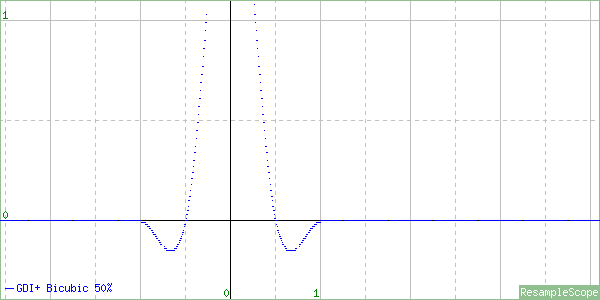
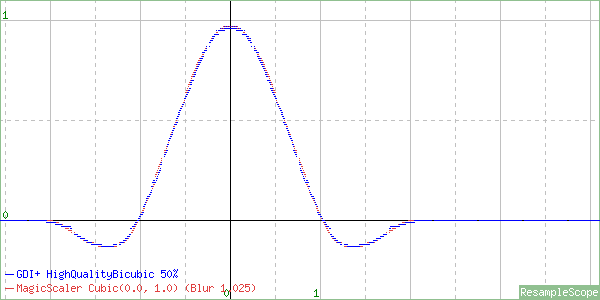
The blur factor will soften edges when enlarging, which can prevent aliasing, so that’s not a bad choice. In fact, This is actually very similar to PhotoShop’s Bicubic Smoother resizing mode. Here’s a shrink to 50%.

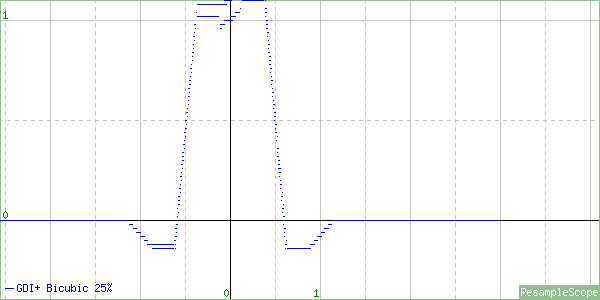
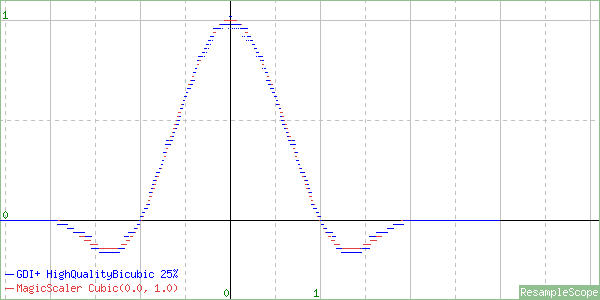
This one looks more like a Cardinal Cubic (B=0, C=1), which can cause some ringing artifacts, with a very slight blur factor of 1.025 balancing that out. And finally a shrink to 25%…

On this one, the blur factor is gone, and we’re left with just a Cardinal Cubic. That seems to hold up at more extreme downscale ratios as well. Again, it sharpens more than some people would prefer and can cause some ringing and moiré, but it’s a correctly-implemented interpolator. It’s certainly the best GDI+ has to offer for shrinking.

Once again the the slight discontinuities in the graphs indicate there may be a pre-blur at work, but they match the reference curves closely, so the results will be very close to correct (for this algorithm).

The Others

Now that we know what all the explicitly named interpolators actually do, it’s a simple matter of comparing the graphs to put real names to the generic ones. Why the docs don’t do this is beyond me, but here goes…

InterpolationMode.Default = InterpolationMode.Low = InterpolationMode.Linear

InterpolationMode.High = InterpolationMode.HighQualityBicubic

That’s it?

Pretty much. GDI+ obviously has a limited selection of interpolators, and the tradeoff in speed between the Default/Low/Linear and the High/HighQualityBicubic is quite dramatic. Adding to that speed difference is the fact that both of the HighQuality interpolators require that the input image be converted to RGBA format for processing, while the Linear interpolator is able to process in RGB mode directly. If you think about resizing a high-res file, that conversion cost could be quite high, not to mention the work done by the interpolator itself. It’s not uncommon in cases of extreme downscaling to use a hybrid approach, where the image is downscaled to an intermediate size using a faster/lower-quality interpolation and then finished off with a high quality interpolator to get to the final size. In fact, MagicScaler does just that with its hybrid scaling modes. Photoshop does too. I didn’t bother implementing that in my reference resizer, but if you’re stuck with GDI+, it might be worth a try for you.

So there you have it… more than you probably ever wanted to know about GDI+’s interpolator implementations. This info will come in handy when comparing GDI+ with MagicScaler, though, as we want to make sure we’re doing the same work in both. Wouldn’t be fair otherwise, would it?

In the next and final installment, I’ll be going over the image ‘validation’ in System.Drawing and looking a bit further into that RGBA conversion I mentioned for the HighQuality interpolators.