When I started the task of creating a minimal sRGB profile, I assumed the part that would require the least thought would be the colorant and whitepoint tags in the profile. To review, the ICC V2 specification requires 9 tags for RGB profiles. Those are: copyright (cprt) and description (desc), which I discussed in Part 1 of this series; the tone reproduction curves (rTRC, gTRC, and bTRC), which I covered thoroughly in Part 2; and finally, the colorant and whitepoint tags (rXYZ, gXYZ, bXYZ, and wtpt), which ended up with their own post, too. This is that post.

I have referenced Elle Stone’s treatise on well-behaved profiles a couple of times already, and I’ll start this post by referring there again. I’ll also refer you to her systematic examination of ICC profiles seen in the wild and finally, to her very detailed explanation of how to create an sRGB-compatible ICC profile using the values from the sRGB spec.

I drew two main conclusions from reading through those articles. The first was that well-behaved and correct sRGB profiles are difficult to create and are, consequently, rare. The second was that the reference sRGB profile shipped with ArgyllCMS happens to be that most mythical of profiles. The unicorn profile, if you will.

And that’s what was supposed to make this step simple; I’d just steal the colorant tag values from the ArgyllCMS profile and call it a day.

Facebook’s TinyRGB profile had used the colorant tag values from the original HP/Microsoft sRGB profile, and while that remains the most commonly-seen sRGB profile in the wild, Elle had convinced me it was also one of the most wrong.

In his writeup on the sRGBz profile, Øyvind Kolås (Pippin) mentioned generating new colorant tag values from babl with improved accuracy. My first assumption was that it must also use those magical Argyll values. Imagine my surprise when I looked at the tag data and saw that they were a completely different set of values. And imagine my further surprise when I ran them through Elle’s xicclu test and found that they were also well-behaved.

That left me with two sets of possible correct sRGB colorant values, and I simply had to know which was right. The rabbit-hole deepens…

Better-Behaved?

If there are two well-behaved sRGB-like profiles with different colorant values, they must not be as difficult to come by as I originally thought. Elle describes creating well-behaved profiles as a process of calculating the most correct values for the colorspace and then ‘nudging’ them so that their rounding errors when converted to the ICC s15Fixed16Number format balance out. I learned that this is actually a very simple process and that testing for well-behavedness is a matter of simple arithmetic. Let’s start with the actual colorant tag values stored in the three profiles I was examining.

      |     HP/Microsoft     |        sRGBz         |      ArgyllCMS     
-------------------------------------------------------------------------
      |     X      Y      Z  |     X      Y      Z  |     X      Y      Z
Red   |  6FA2   38F5   0390  |  6FA1   38F6   0391  |  6FA0   38F5   0390
Green |  6299   B785   18DA  |  6297   B787   18DA  |  6297   B787   18D9
Blue  |  24A0   0F84   B6CF  |  249E   0F83   B6C2  |  249F   0F84   B6C4
Sum   |  F6DB   FFFE   D339  |  F6D6  10000   D32D  |  F6D6  10000   D32D

I’ve kept the values in hex for now, because 1) I read them out with a hex editor and 2) it’s easier to see what’s up when looking at the integer representation of the numbers. What the table above shows is the XYZ values for the Red, Green, and Blue primaries stored in each of the three profiles I examined. I also included a row that shows the sum of the X, Y, and Z values for the three color channels. One thing should stand out immediately: the sRGBz and ArgyllCMS color values are different, but their sums are the same. What’s not obvious from the table is what those sums represent.

First, let me explain how the color values are stored in an ICC profile. The ICC spec defines the s15Fixed16Number format for storing XYZ (and other) values. In that format, 16 bits are allocated to the signed integer portion of the number and 16 bits are allocated to the fractional part of the number. The conversion between floating-point decimal and the fixed-point format is simply to multiply by 2¹⁶ and round to the nearest integer. Conversion back to floating-point decimal is done by dividing by 2¹⁶ (65536). In that format, 1.0 is represented by 0x00010000 because its integer part is 1 and it has no fractional part.

This is in contrast to the response16Number format used to store the TRC points we examined in the last post. In that format, 16 bits are used to represent the full range of 0-1, inclusive. For that number format, the divisor is 2¹⁶-1 (65535), so that 1.0 is represented by 0xFFFF. This has come up as a point of confusion in some things I’ve read, so I thought I’d clear that up.

Now back to the values in the table…

Every developer who works with RGB colors knows that in 8-bit color, black is [0,0,0], full red is [255,0,0], etc. We also know that if you add full red, full green, and full blue together, you get [255,255,255], which is white. Things work the same in XYZ. Adding the three primary colors together at their full intensity (as defined within the colorspace) will give you white (also as defined in the colorspace). In most practical colorspaces, the XYZ values are normalized so that white has a Y value of 1.0. In some representations, you may see the XYZ numbers scaled up to a range of 0-100, but both the ICC and sRGB specs declare that the nominal range is 0-1.

Knowing that white should have a Y value of 1.0 and that 1.0 in s15Fixed16Number format is 0x10000, you should see an immediate problem with the values in the HP/Microsoft sRGB profile: their Y values sum to less than 1.0, meaning they’re scaled improperly.

Its X and Z values are wrong as well. The ICC V2 spec requires that all profiles have their color values adapted to the D50 whitepoint, which allows for simple translation between colorspaces. Since XYZ conversion to and from RGB is whitepoint-dependent, using a common whitepoint for all profiles makes it easy for software to implement that translation. As an aside, let me point out that RGB values we are referring to linear RGB values. That is, the red, green, and blue values that are the output of the TRC that undoes their stored gamma correction. Those values are also normalized to the range 0-1 for computation.

The ICC spec is explicit about the XYZ value to use for the D50 whitepoint, giving it a value of [X=0.9642,Y=1,Z=0.8249]. When converted to s15Fixed16Number format, that value becomes [X=0xF6D6,Y=0x10000,Z=0xD32D], which is the exact value stored as the Profile Illuminant in the header of every V2 ICC profile.

If you refer back to the table of values from the three profiles I examined, you will find that the sRGBz and ArgyllCMS primary colorant values sum to exactly the value of the D50 Illuminant given by the ICC. Put simply, that’s what makes a profile well-behaved. And you can see that the HP/Microsoft profile is quite far off from that value, which is why it’s no good.

Knowing that making a profile well-behaved is simply a matter of normalizing the primary colors so that they sum at full intensity to make white, it’s easy to see how we ended up with two different sRGB-like profiles that are both well-behaved. But that still leaves the question of which is right.

In Which I Learn They’re Both Wrong

It’s been a while since I linked to Nine Degrees Below, so let me start this section with another link to Elle’s research into the proper color values to use for sRGB. In that article, Elle rounds up every possible definition of every color referenced in the sRGB spec, does every bit of mathematical wrangling imaginable, and comes up with a final set of numbers that are very close to the ones that ArgyllCMS has in its reference sRGB profile. Score one for Argyll.

I decided to do a similar exercise and find my own answer to compare to the others. One problem with making things match the sRGB spec is that the spec itself isn’t published freely. If you want to read the actual spec, it will cost you 170 Swiss francs to buy it from the IEC web store.

Fortunately, there are enough references available elsewhere that I believe we can put together an accurate picture of the spec without ponying up. I like to save my francs for Swiss chocolate and wine, thank you very much. I can enjoy those while I read the Wikipedia entry on sRGB.

At this point, it’s worth considering exactly what numbers we’re trying calculate. Depending where you look you may see the colorant values described in one of two ways:

1. They represent the direct XYZ translation of the three primary colors (red, green, and blue) at their full intensity under the specified illuminant.
2. They make up a matrix which can be used to translate any set of [R,G,B] values to their corresponding [X,Y,Z] values.

In reality, both are correct. But I think for our purposes, it’s important to focus on the second definition. The reason that’s important is that the colorant values stored in the ICC profile are used in exactly that way. They’re also used in another, related way. The matrix created from those XYZ colorant values can be inverted to create the matrix that translates from XYZ back to RGB. This will become very important later, so I wanted to mention it now and let it soak in a bit.

If you use a tool like the Profile Inspector available on the ICC site, it reinforces the first definition I gave. They show the XYZ values converted to decimal, the calculated x and y coordinates for that color, and a nice chromaticity diagram with the color plotted on it. Here’s the rXYZ tag information from the Argyll sRGB profile.

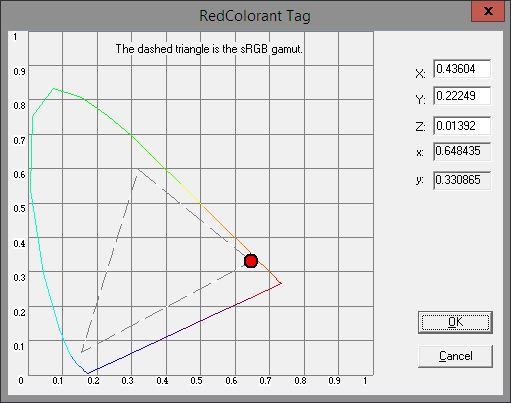
Exiftool, on the other hand, presents the data using the second definition. Here’s the relevant output from the same profile:

Red Matrix Column:   0.43604 0.22249 0.01392
Green Matrix Column: 0.38512 0.71690 0.09706
Blue Matrix Column:  0.14305 0.06061 0.71393

You can see that the XYZ values are the same in each, and that makes perfect sense. If you make a matrix using the columns given by Exiftool

0.43604 0.38512 0.14305
0.22249 0.71690 0.06061
0.01392 0.09706 0.71393

and then multiply the linear value for pure red [1,0,0] by that matrix, you get the left column back, giving you the same XYZ value shown for the red primary in the Profile Inspector. Again, it’s the same thing… but the matrix usage is the more important definition.

So, that leaves the question: how do we calculate that matrix, given the values in the sRGB spec?

That answer has two parts. For the first part, we must get the matrix for converting RGB to XYZ using sRGB’s native illuminant/whitepoint, which is D65. Then, because the colors in an ICC profile must be given relative to the D50 illuminant, we must adapt that matrix from D65-relative values to D50-relative values. Bruce Lindbloom has a reference on the basic theory of Chromatic Adaptation as well as some different adaptation matrices on his site. But I’ll caution you not to use his pre-calculated matrix for D65->D50; it’s wrong for our purposes.

Let’s start with the matrix for calculating RGB->XYZ under D65. The Wikipedia article on sRGB has the matrix printed right in it. It also points out explicitly that the values listed are the exact ones in the sRGB spec. Again, I don’t have the actual spec, but I have no reason to doubt the veracity of that statement. The sRGB spec reportedly is full of exact numbers, rounded to 4 decimal places.

Well, like Elle, I started with the assumption that more precision is better, and I didn’t like the look of those imprecise numbers from the spec. So, like Elle, I tried to calculate my own more precise matrix using the the published x,y values of the primaries. That effort was a complete failure. What I mean is, while I succeeded in the calculation, if I then inverted my matrix to create the XYZ->RGB matrix, it didn’t match the one in the spec to the 4 decimal places it has listed. It turns out, the best way to get the correct (according to the spec) inverse matrix is to use the explicitly rounded values given in the RGB->XYZ matrix.

0.4124  0.3576  0.1805
0.2126  0.7152  0.0722
0.0193  0.1192  0.9505

Invert that, and you get

 3.2406254773200500 -1.5372079722103200 -0.4986285986982480
-0.9689307147293190  1.8757560608852400  0.0415175238429540
 0.0557101204455106 -0.2040210505984870  1.0569959422543900

Which matches the spec (as described by wiki) very nicely, and with lots of decimal places, if that’s your thing. Round that back to 4 decimal places, like such, to match the spec again,

 3.2406 -1.5372 -0.4986
-0.9689  1.8758  0.0415
 0.0557 -0.2040  1.0570

Invert that, and you get

0.4124103360777000  0.3575962178119540  0.1804991017305060
0.2126157251481260  0.7151958779229800  0.0722134074030765
0.0193021307575116  0.1191881265507680  0.9504992763896300

Which, again, rounds to match the spec at 4 decimal places. These, I’m confident, are the correct numbers for sRGB at D65, which just leaves the D65->D50 adaptation matrix to work out.

This, again, seems like a place where more precision would pay off, but in fact, there is a value listed in the spec, rounded to 4 decimal places, that is perfect for this use. That value given for D65 is [X=0.9505,Y=1,Z=1.0890]. We also have a standard XYZ value for D50, given by the ICC spec. That value is [X=0.9642,Y=1,Z=0.8249].

As an aside, you may recall that the actual D50 value stored in the profile header is in s15Fixed16Number format and is, in hex [X=0xF6D6,Y=0x10000,Z=0xD32D]. Converted back to floating-point decimal, that value is [X=0.964202880859375,Y=1,Z=0.8249053955078125]. If you want to be extra precise, that value is also acceptable to use. It worked out that when creating the adaptation matrices, it didn’t matter which number I used. I got the same results once the quantization to s15Fixed16Number format was done for the final calculated values. For the calculations shown below, I used the rounded value published in the ICC spec.

Using the D50 XYZ value from the ICC spec, the D65 XYZ value from the sRGB spec and the Bradford cone response matrix given by Bruce Lindbloom, we get the following values for the D65->D50 adaptation matrix:

 1.0478414713468100  0.0228955556744975  -0.0502009864000404
 0.0295477450604968  0.9905065286192130  -0.0170722316797199
-0.0092509594572860  0.0150723678359253   0.7517177861599870

Notice that the matrix I calculated is different than the one Bruce gives on his site:

 1.0478112  0.0228866 -0.0501270
 0.0295424  0.9904844 -0.0170491
-0.0092345  0.0150436  0.7521316

They’re quite close, but he used D65 and D50 values from a different source. It comes down to rounding differences, but remember, we’re following exact specs, so we want to round the same way they do.

And finally, if we multiply our RGB->XYZ matrix by the adaptation matrix, we get the final adapted values:

0.4360285388823030  0.3850990539931360  0.1430724071245600
0.2224376839759750  0.7169415328858720  0.0606207831381531
0.0138974429946207  0.0970763744845987  0.7139261825207810

Converted to s15Fixed16Number format, written in hex, and transposed to match the profile layout I used earlier, those numbers look like this:

      |     X      Y      Z
Red   |  6FA0   38F2   038F
Green |  6296   B789   18DA
Blue  |  24A0   0F85   B6C4
Sum   |  F6D6  10000   D32D

You’ll note that the hex values exactly total those of the D50 Profile Illuminant, so these values will create a well-behaved profile. These values, however, do not match any other profile I’ve seen.

I also found that the D65 whitepoint stored in most profiles doesn’t match the sRGB spec value. The XYZ values given in the spec, again, are [X=0.9505,Y=1,Z=1.0890], which in s15Fixed16Number hex are [X=F354,Y=10000,Z=116C9]. All sRGB profiles I’ve examined (if they define a D65 whitepoint) have had the following value for the ‘wtpt’ tag [X=F351,Y=10000,Z=116CC], which works out to [X=0.9504547119140625,Y=1,Z=1.08905029296875].

I’m convinced my numbers are the correct colorant and whitepoint values for sRGB as written in the actual spec. But you may be reluctant to take my word for it, especially given that there are so many other profiles out there with different values. Fortunately, I have a bit of official documentation on my side.

While trying to locate the most correct and precise definition of the D65 and colorant values available, I ran across a document entitled “How to interpret the sRGB color space (specified in IEC 61966-2-1) for ICC profiles”. I wonder what it’s about....

That document is published on the ICC website, under its information page for sRGB.  For some common colorspaces, the ICC publishes spec extension documents that describe how to treat that specific colorspace in the context of a profile. That document is linked at the bottom of the page, under Hints for Profile Makers.

If you read through that document, you will find the same rules and numbers I used, extracted from the sRGB spec (which I assume the ICC has an actual copy of). For example, section A7 contains the exact XYZ->RGB matrix I listed above. Theirs has more decimal places than the Wikipedia page but less than mine. You’ll also find under section B2, the exact recommended D65->D50 Bradford adaptation matrix. Theirs only matches mine to 5 decimal places, but I think mine came out better, because… hold the phone.. they included the actual suggested ICC profile matrix, with many decimal places of precision. You’ll find that is also very close to mine. In fact, when converted to s15Fixed16Number format in hex as I’ve done with the others, those numbers are:

      |     X      Y      Z
Red   |  6FA0   38F2   038F
Green |  6296   B78A   18DA
Blue  |  24A0   0F85   B6C4
Sum   |  F6D6  10001   D32D

You can see they are identical to mine from above with the exception that the Green Y value came out 1 higher, making the sum 1 too high. That’s within nudging distance of being well-behaved, but I believe that if their adaptation matrix had been a bit better, the nudging wouldn’t have been required; it wasn’t with mine.

The existence of that document on the ICC site begs the question: are they using those values in their reference sRGB profiles? The answer is no. No, they are not. Their profiles, as of today, are still using the same busted numbers from the old HP/Microsoft profile. I don’t know why.

So, that’s the mathematical explanation of how I arrived at my profile color values and a bit of evidence to support their validity. But maybe you’re still not convinced. There are, after all, two different definitions of the D65 value and two different versions of the primary color values given on the Wikipedia page for sRGB. Wouldn’t a profile created with those other numbers also comply with the spec? Well, no, actually. And I’ll do the math to show you why. But first a bit of history.

The Life of sRGB

sRGB started its life as a derivative of the Rec. 709 HDTV standard. The authors, who came from HP and Microsoft, took the primaries/gamut and whitepoint/color temperature from the Rec. 709 standard, modified the gamma curve to more closely match the response curve of CRT-based computer displays, and created their own draft spec. That draft is still available online today.

Despite the large red warning at the top of that page that explains it is obsolete, you will still find values from that draft spec living on in modern software. This is, no doubt, partly a result of the fact that the draft is freely available and the actual spec has to be purchased.

Basically, what happened was that the draft authors rounded most of the numbers they used when they published them. This, in turn, led to inaccuracy in several parts of the draft spec. When the draft was submitted to the IEC for standardization, it went through a process of refinement wherein that inaccuracy was resolved before the spec became final. In many cases, the resolution was a slight tweak of the numbers to cancel out the rounding errors or to bring things back into alignment.

One such example of this is nicely documented on the sRGB Wikipedia page, in the section entitled “Theory of the transformation”. That section describes how the original intended values for the response curve produced numbers with lots of decimal places. Those numbers were rounded in the draft spec, creating a break in the curve at the transition from its linear portion to the actual gamma curve. The numbers were then adjusted for the final spec to resolve the break. The adjustments fixed the error in the sense that the two parts of the curve were made to meet up again, but they also changed the curve segments such that although they meet, the slope of the lines is no longer continuous as was originally intended.

That refinement is a bit of a recurring theme in the sRGB spec, where the intended value and the actual value published are different. This happened with the definitions of the color values and whitepoint as well. There is a note in the section describing the XYZ->sRGB transformation that reads

“The numerical values below match those in the official sRGB specification, which corrected small rounding errors in the original publication by sRGB's creators”

Essentially, what that means is that in the final spec, the XYZ values for the D65 illuminant and the XYZ transformation matrices have been adjusted to compensate for the 4-decimal-place rounding that was used on the original draft spec numbers. If you use those rounded numbers from the draft, you’ll get incorrect results. If you use the intended numbers, you’ll get results that are mathematically correct but are incorrect according to the published spec.

And that leads us back to the colorant and whitepoint tags in the ArgyllCMS reference sRGB profile. I’ll do the math that leads to those numbers so I can show you where they deviate from the standard.

How Not to Create an sRGB ICC Profile

I mentioned earlier that my quest for additional precision beyond that given in the sRGB spec led to a dead-end. I’ll go through that path again to show why. Let’s start by assuming that the XYZ values given for both the D65 illuminant and for the primary colors (by way of the RGB->XYZ transformation matrix) are not good enough. That leaves us with the alternate definitions of those values, which were copied directly from the Rec. 709 standard. They are defined on the sRGB Wikipedia page as follows:

  Red     Green   Blue    White(D65)
x 0.6400  0.3000  0.1500  0.3127
y 0.3300  0.6000  0.0600  0.3290
Y 0.2126  0.7152  0.0722  1.0000

Cross-referencing the Rec. 709 standard, which is freely available, the red, green, blue and whitepoint x and y values all match, except Rec. 709 only defines the color chromaticity coordinates to 2 decimal places (those extra 0’s are filler). The Y values given do not appear in the Rec. 709 spec, and that’s because 1) they can be calculated from x and y if you know the whitepoint and 2) those values are rounded to 4 decimal places, which makes them less precise than they could be if we calculated them.

Bruce Lindbloom has tons of useful color-related math on his site, and I referred to his Chromatic Adaptation page/formulas/matrices earlier. This time I will refer to his page on generating XYZ/RGB matrices.

Remember, the RGB->XYZ matrix and the primaries are the same thing, so if we get the matrix, we’ll have the precise XYZ values for our color primaries. The formula on that page starts by converting each xy color to unscaled XYZ, by setting its Y value to 1 and calculating X and Z from there. It then uses the whitepoint, which we know should have a Y value of 1, to compute a scaling factor (the S vector), which defines the final component colors relative to that white. To get the whitepoint’s XYZ value, we can use this formula, or we can use the simplified version on the matrix calculation page since we know the Y value is 1. That gives us an XYZ value for D65 of [X=0.950455927051672,Y=1,Z=1.08905775075988]. Now that’s some decimal places!

Using that value to compute the RGB->XYZ matrix, we get the following:

0.4123907992659590 0.3575843393838780 0.1804807884018340
0.2126390058715100 0.7151686787677560 0.0721923153607337
0.0193308187155918 0.1191947797946260 0.9505321522496610

And rounding that to 4 decimal places, we get the exact numbers listed in the sRGB spec (I’ve been informed by a Wikipedia author)

0.4124  0.3576  0.1805
0.2126  0.7152  0.0722
0.0193  0.1192  0.9505

Plus, we have extra precision, and we love extra precision. Everything is awesome! Now, let’s create an extra-precise Bradford adaptation matrix to go from our extra-precise definition of D65 to the ICC’s specified D50 value. Here’s the adaptation matrix

 1.0478860032225500  0.0229187651747795 -0.0502160953117330
 0.0295817824980035  0.9904835184905490 -0.0170787077044827
-0.0092518808392088  0.0150726074870313  0.7516781336176040

And the final D50-adapted RGB->XYZ matrix

 0.4360412516160510  0.3851129107981560  0.1430458375857940
 0.2224845402294770  0.7169050786084580  0.0606103811620653
 0.0139201874713754  0.0970672386971240  0.7139125738315010

Converted to profile format, it’s an exact match for Argyll’s sRGB

      |     X      Y      Z
Red   |  6FA0   38F5   0390
Green |  6297   B787   18D9
Blue  |  249F   0F84   B6C4
Sum   |  F6D6  10000   D32D

It’s well-behaved, it’s precise (or at least it was until we quantized it for the profile), and we got it using numbers from our telephone-game version of the spec. So what’s wrong with it? Well, let’s back up a couple of steps to the unrounded, unadapted D65 RGB->XYZ matrix. If we invert that to create the XYZ->RGB matrix, this is what we get:

 3.2409699419045200 -1.5373831775700900 -0.4986107602930030
-0.9692436362808800  1.8759675015077200  0.0415550574071756
 0.0556300796969936 -0.2039769588889760  1.0569715142428800

And here again is the XYZ->RGB matrix from the spec – as described to me by a little birdy.

 3.2406 -1.5372 -0.4986
-0.9689  1.8758  0.0415
 0.0557 -0.2040  1.0570

Notice that these matrices no longer agree to the 4 decimal places of precision defined in the spec. If we go back and look at the draft spec, we can see that it lists a different set of rounded numbers, which do match

 3.2410 -1.5374 -0.4986
-0.9692  1.8760  0.0416
 0.0556 -0.2040  1.0570

And therein lies the problem. These rounded numbers from the draft spec don’t invert to create the correct RGB->XYZ matrix. Here’s that one:

 0.4123808838269000  0.3575728355732480  0.1804522977447920
 0.2126198631048980  0.7151387878413210  0.0721499433963131
 0.0193434956789248  0.1192121694056360  0.9505065664127130

We have a round-trip failure, caused by the lack of precision. To fix that, the spec (which I once saw a blurry photo of, I swear) was modified and the values adjusted so that at 4 decimal places of precision, each matrix inverts to the other. Defining the RGB/XYZ matrices such that they work with only 4 decimals of precision has another benefit that we didn’t get to see. The D65 XYZ values I used were carried through all calculations with full double float precision as well, so there was no opportunity for our whitepoint to throw the other colors off balance. Without that precision, it’s difficult to maintain balance, which I assume is how the HP/Microsoft sRGB profile ended up so bad.

Using the rounded XYZ values for the primaries, you’ll find that they add to exactly the rounded value given for D65.

      X       Y       Z
Red   0.4124  0.2126  0.0193
Green 0.3576  0.7152  0.1192
Blue  0.1805  0.0722  0.9505
White 0.9505  1.0000  1.0890

This creates automatic balance, even with a low level of precision, which was the intent. You may have noticed that this required rounding the Z value of of the whitepoint in the wrong direction. The more precise calculation of the whitepoint we made above gave D65 a Z value of 1.08905775075988, which should have rounded to 1.0891. Oddly enough, the D65 Z value is listed both ways in the draft sRGB spec. But it works out that rounding it down to 1.0890 makes everything work better, so that’s what ended up in the final spec (I think I overheard a guy mutter to himself on the bus one time).

And now I’ll do one final conversion to prove these rounded numbers are the bestest: let’s convert them to xyY, and see if they match the intended Rec. 709 colors.

      x                  y                   Y     
Red   0.640074499456775  0.329970510631693   0.2126
Green 0.3                0.6                 0.7152
Blue  0.150016622340426  0.0600066489361702  0.0722
White 0.312715907221582  0.329001480506662   1.0

Sure enough, round those to the requisite 2 decimal places for colors and 4 for white, and they match the spec values exactly.

So what we learned is, if you use the xy color values inherited from Rec 709, you’ll match the original intent of the draft spec, but you won’t match the actual final spec. For that, you must use its final XYZ numbers with their intentional imprecision. That’s how I got my numbers, and I’m stickin’ to ‘em.

That leaves just one step in my journey to the perfect compact sRGB profile. Come back for the final post, where I’ll compare my final profiles with some references and see which one gives the best bang for your buck.

Update: A Bit of Perspective

After I published this post, Graeme Gill (the creator of ArgyllCMS) commented here, and then he and Elle Stone and I had a bit of further discussion on the pixls.us forum.

Those exchanges led me to think a little more clarification is necessary on this topic. It turns out to be quite controversial, at least among people who have spent any significant time thinking about it (we are likely few in number). And I heard from a couple more people who found the topic interesting but didn’t have the background knowledge to follow everything completely. Talking to them gave me some better ideas for explaining the disagreement, so I thought I’d get them written down.

But I want to get two things straight before I get back into the details.

First, I think a bit of perspective is in order. I said that Graeme and Elle’s reference sRGB profiles (they match in primaries and whitepoint) were wrong. There are varying degrees of wrong, and I want to make it clear that although I think their profiles are wrong according to my interpretation of the sRGB spec, I believe they are correct according to their own interpretations. When I took an alternate approach to deriving the colorant and whitepoint values, using math that I believe to be 100% correct but with inputs I don’t agree are correct, I got numbers that match the ArgyllCMS sRGB profile. That contrasts starkly with the HP/Microsoft sRGB profile, which all three of us agree is wrong in a much more significant sense. I believe the ArgyllCMS sRGB profile is better described as a Rec. 709 profile with sRGB TRCs. Graeme argues those are the same thing.

Second, even though the raw numbers might have looked far apart when I presented them before, they were given with an absurd number of decimal places, especially given their target use. Once they end up in an ICC profile, most of those differences are quantized away. Only first log₁₀(2¹⁶) decimal places are accurately preserved in s15Fixed16Number format, which amounts to 4 decimal places reliably. In the end, the level of disagreement between our interpretations of the sRGB spec has a maximum net impact on our final profile values of 3/65536, or 0.0000457764 on any given number. So while we may argue our interpretations of the spec, we’re arguing over a difference that likely won’t ever be visible in any image.

Update 2: I have finally seen the spec!

I had a section here that further explored the different interpretations possible from the partial information publicly available, but it was a bit rambly and included more conjecture. I have removed it in favor of a new post, which explains what I learned from reading the real deal.